Intervals (not only) in Diatonic Chords

We started this whole section talking about the diatonic context as something essential. As well we said something about intervals in the article ... We mentioned something about their relation to the diatonic context too .... The truth is that in the final consequence musical harmony is based on intervals and their connections. Diatonic context is only a means and a tool for us to look at intervals some synoptical way, a tool to grasp musical units and mentally work with them, to remember them, to sort them somehow. But the music is created by intervals and thus we should start realizing them and appreciating them more - in the diatonic context. In other words we can say that diatonic view and interval view are two complementary perspectives. While diatonic view helps us to work with larger wholes, interval view offers understanding details.

Thus we need to look at intervals not only in general in diatonic context, as we have done already, but more specificaly in (diatonic) chords. And we should consider something what we could call a simple interval arithmetic.

Intervals in Chords: What types of basic chords we have? First we have triads. Minor and major. We will look at diminished too. Then we have four-note chords (seventh chords). They are extensions of triads. In the diatonic context we have major major, major dominant and minor dominant chords. To have the set more complete, we will add two more types - minor major and diminished. And we will look at intervals in them. First the triads (We will look at intervals among all their tones. It is important not only because chords can appear in inverted positions, but because they appear in reduced forms too):

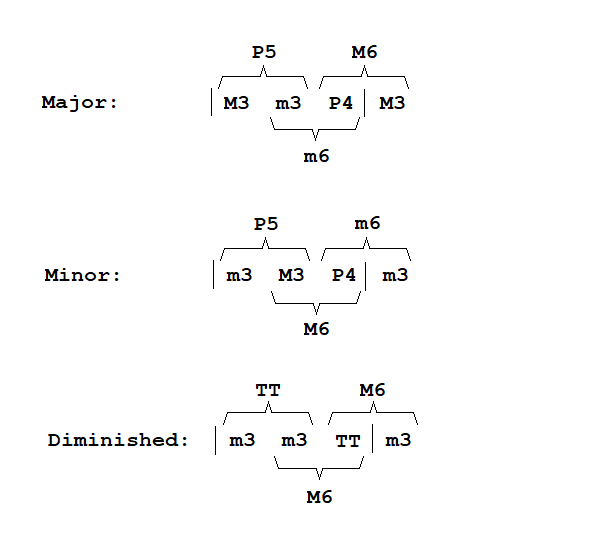
Here we see all the intervals that can occur in the context of the mentioned triads. What interval-arithmetic knowledge can we take away?

M3 + m3 = P5
m3 + P4 = m6
M3 + P4 = M6
m3 + m3 = TT
m3 + TT = m3 + m3 + m3 = M6

Now let's look at seventh chords and all the new intervals that they bring:

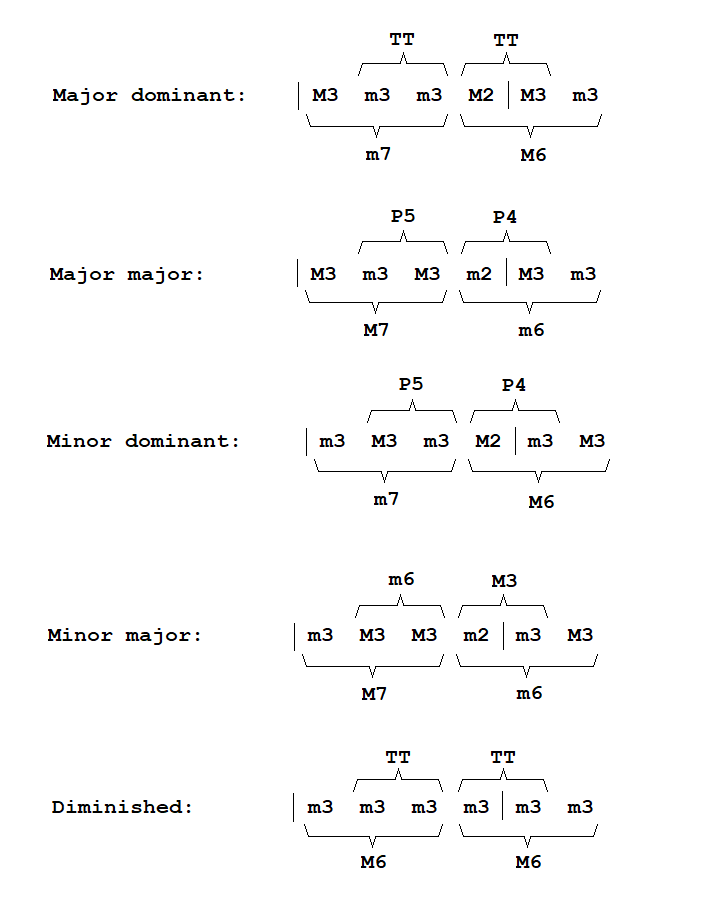
We can extend our ruleset as follows:

M2 + M3 = TT
P5 + m3 = M3 + m3 + m3 = m7
P5 + M2 = M3 + m3 + M2 = M6
m2 + M3 = P4
M2 + m3 = P4 
P5 + M3 = M3 + m3 + M3 = M7
M3 + M3 = m6
m2 + m3 = M3
P5 + m2 = M3 + m3 + m2 = m6

What is all this good for? For better orientation in analysed pieces. We don't say you should start memorizing these rules now as a multiplication table. We just think that sooner or later, if you analyze the music you play, you will need and you will have this ruleset in your head. It is better to learn it while working on the keyboard than from the paper. But sometimes a paper can be helpful.